A Heuristic Approach to Calculating Geometric Medians

I was recently given an interesting problem:

Given a set of points in on a common plane ​$P$, find a point ​$Q$ on ​$P$ that minimizes the net cost of traveling from ​$Q$ to each other point.

Ignoring the problem of calculating costThe differences between traveling by car, bike, and foot include important time and cost differences. Here, we'll employ Euclidean distance as an uncomplicated, normalizing cost function., this problem may seem fairly straightforward. Let's look at some approaches.

0: ​$Q$ as the Median

As it happens, the median of a set of points is guaranteed to be the cost-minimum center of those points only in ​$\Bbb{R}^1$ space. We can show that the median does not hold in ​$\Bbb{R}^2$ via a counter-example: create a triangle with vertices ​$[(0, 0); (0, 1); (1, 0)]$, the median of which is at ​$(\frac{1}{3}, \frac{1}{3})$:

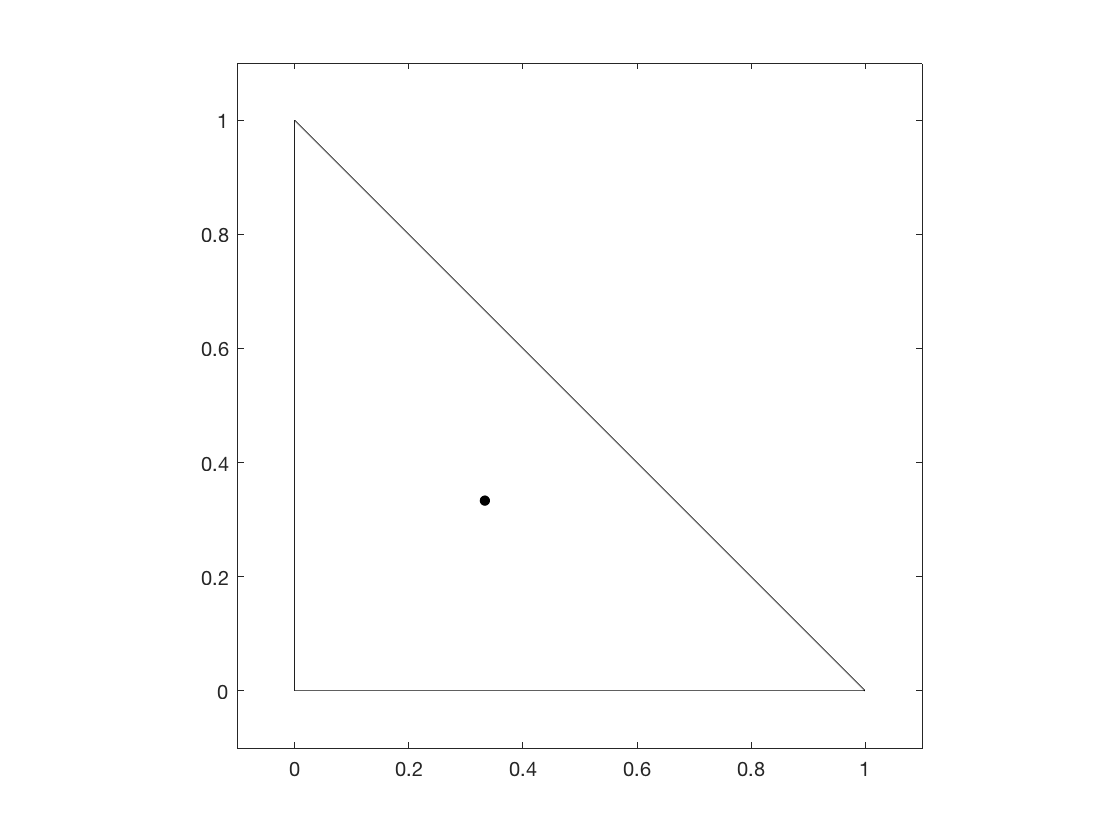
The net cost of traveling from the vertices to the center point can be improved by ​$1.54%$ if we make that center point ​$(0.211, 0.211)$:

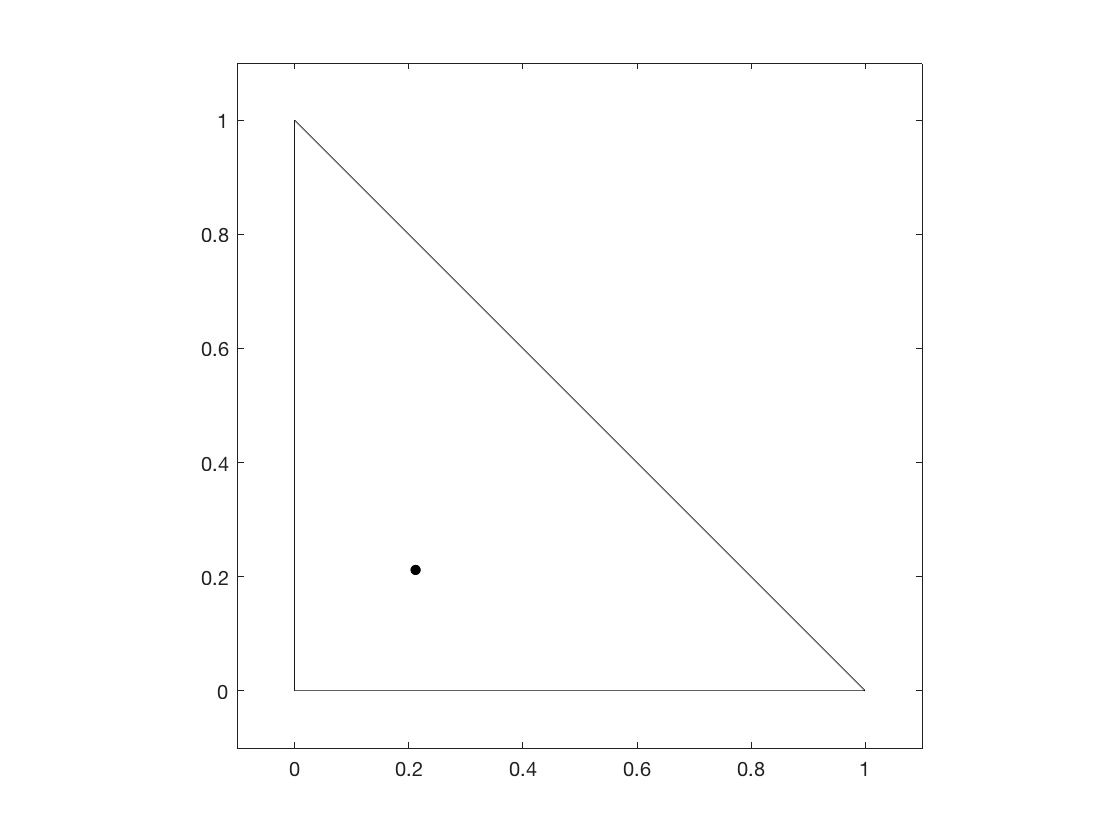
For most, ​$1.54%$ isn't all that much, and the median is a pretty good approximation for the latter point - the geometric median More info., or center as I will refer to it from here. But what if the percent improvement grows higher, say to ​$5%$ or ​$10%$ or ​$20%$? How do we derive this geometric median?

1: Function Minimization

What if we attempt to minimize the net cost function? Say that for some point ​$Q = (Q_x, Q_y)$, the net cost of traveling from a set of points ​$n$ with coordinate form ​$(x, y)$ to ​$Q$ is

Hey, pretty good! Let's do ​$\frac{\partial}{\partial Q_x} = 0$, ​$\frac{\partial}{\partial Q_y} = 0$, throw in a second derivative test, and call it a day.

Oh man. Maybe not. That looks like a pain in the ass to solve for ​$Q_x$, let alone simultaneously with ​$\frac{\partial}{\partial Q_y}$⊕I have no idea how to do this efficiently, but if you do, please let me know. Looks like it could be worth a lot of money!. Don't forget this process would have to be automated, too - wow that looks fun!

2: Heuristic Approximation

You know the old saying:

If you can't derive 'em, approximate 'em!

...and so heuristics come to the rescue! How? Well, a good place to start is WolframAlpha a contoured version of the function whose extrema are in question.

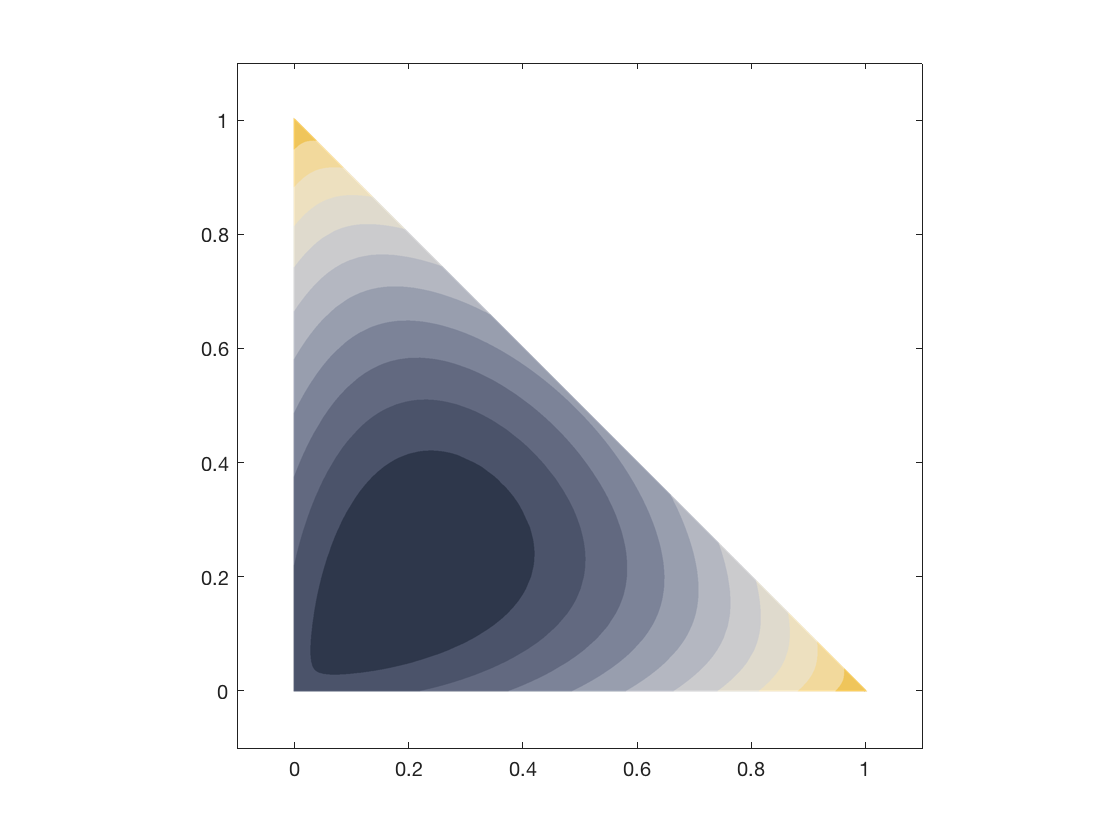
As expected, the contour slopes in around the previously-shown minimum ​$(0.211, 0.211)$. Interestingly, there seems to only be one minimum for this function - and in general, there is only one centerSee this paper, which shows that the geometric center is unique and convergent for any set of non-co-linear points. for any set of points! This means we can employ some descent-type optimization method.

Okay, but where do we descend from?

A convenient place would be from the median. It's cheap to compute and fairly close to the center.

How do we descend?

This is a bit trickier. Of course, we can only travel in ​$\Bbb{R}^2$, so let's just say we can go up, down, left, or right⊕Formally, +y, -y, -x, or +x. A more thorough traversal could also employ diagonal directions.. To find the best direction of descent, we travel to a candidate point in each direction and determine the one that most improves the cost.

What if no direction lowers the cost?

Then we've found our center! Except we could probably do better, by decreasing our search radius and repeating the descent mechanism again. And again, and again, until the approximation of the geometric center is within some acceptable margin of error ​$\epsilon$.

Alright, let's code it!⊕These examples are in Rust, but it should be easy to implement the logic in any language of your choice. The full code can be found here, with a C version here. First, the boilerplate - a euclidean cost function.

400: Invalid request

And now, we can use the previously-defined specification to write a complete algorithm.

400: Invalid request

Let's plug in our three points from before, and...

[0.21126302083333331, 0.21126302083333331]

Awesome!

n: Some Details

This function runs in ​$O\left(\log n\right)$ timeA method for exact computation of the geometric center in near-linear is proposed here., and its precision can be improved by reducing ​$\epsilon$ (epsilon) to an arbitrary minimum.