Type Inference for Sound and Complete Flow Typing

• The FT calculus
  • Pearce's subtyping algorithm
  • $\infer$: type inference for FT
• Preliminaries
• Inferring single variables
  • Bounds
  • Solution sets
  • Existence and construction of $\infer1$
• Dealing with cycles
  • Solution orders
  • Solving for minimal types
  • Putting it all together
• Conclusion
  • Takeaways

An implementation of the type inferer can be found on GitHub. We have also provided a playground that infers and checks FT programs.

The FT calculus

David Pearce's 2012 paper Sound and Complete Flow Typing with Unions, Intersections and Negations develops a subtyping operator for a simple FT (flow typing) calculus, consisting of the proper types

$\any$ is the top type, $\never$ is the bottom type, $\int$ is the type of integers, and $\left(\T_1, \ldots, \T_n\right)$ is a tuple type. $\lnot\T$ is a negation type, inhabited by all values in the universe not inhabited in $\T$. $\T_1 \land \ldots \land \T_n$ is an intersection type, inhabited by values of type $\T_1$ and $\T_2$ and $\ldots$ and $\T_n$. $\T_1 \lor \ldots \lor \T_n$ is a union type, inhabited by values of type $\T_1$ or $\T_2$ or $\ldots$ or $\T_n$.

The syntax of FT is defined on page 4 of Pearce's paper, and restated belowOur syntactic specification differs mildly from Pearce's in that we permit declarations with multiple formals and use a post-fix type annotation syntax.:

All types except $\never$ and $\lnot \T$ are typable by the user; the latter two are generated during flow typechecking. The flow typechecker narrows variable types at checked sites; the $\tt if\ x\ is\ \T$ construct above, for example, narrows $x$ to $\T$ in the $\tt then$ branch, and to "everything except $\T$", $\typeof\ x\ \land\ \lnot\T$, in the $\tt else$ branch. Another unique feature of the flow typechecker is that applications are checked by inlining argument types into a function body and then checking that body, rather than computing a universal return type once.

As a larger example, consider the FT program

fn f(x: any) =
  if x is int|(int, int)
  then 9
  else x
in (f 1, f (1, 2, 3))

First we check the declaration f, where x will be typed as $\int\lor(\int,\int)$ in the then branch, and $\any\land\lnot(\int\lor(\int,\int))$ in the the else branch. When checking the application f 1, we first check if $\typeof\ \mathtt{1}$ is a subtype of $\any$ (using a subtyping operator $\st$, described below), then check the body of f with $x\co\typeof\ \mathtt{1}$ to determine the resulting type of the application. At the conditional, we check if $\typeof\ x$ is a subtype of $\int\lor(\int,\int)$. According to the result, we update the environment and check the appropriate branch.

Pearce's subtyping algorithm

The crucial contribution of Pearce's paper is the construction of a subtyping operator we will call $\st$, under which all of the following hold:

Designing $\st$ to be soundSoundness means no term is illegally subtyped: $\T_1\st\T_2\implies\forall x\co\T_1, x\co\T_2$. and completeCompleteness means the subtyping operator admits all subtypable terms: $\forall x\co\T_1, x\co\T_2\implies\T_1\st\T_2$. is not trivial, and Pearce's paper is a very well-written account of constructing a (semi-)practical$\st$ requires rewriting types to their Disjunctive Normal Form, which can require an exponential amount of time. This is catastrophic in the presence of large or nested tuples, whose DNF rewriting experiences a tremendous explosion in the number of steps. For example, our implementation has been unable to terminate normalization of $(((\int,\int)\land\lnot\int, (\int,\int)\land\lnot\int), ((\int,\int)\land\lnot\int, (\int,\int)\land\lnot\int))$ even after several minutes. Nevertheless, $\st$ is more than suitable for less pathological types. algorithm that is exactly so.

$\infer$: type inference for FT

In this cc, we will design a type inference algorithm $\infer$ that "fills in" omitted type annotations in an FT program. Rather than being a component of the typechecker, $\infer$ is an out-of-band tool that does its best to complete a FT program with annotations demanded by the syntax, which a developer may find cumbersome to write. Indeed, we will prove that $\infer$ is complete, being able to infer every typable FT program; sound, annotating only those programs that are typable; and minimal, always inferring the smallest legal type. In the most extreme case, like ML, $\infer$ can type a program with no annotations at all.

It is not necessary to understand the operation of $\st$However, we will again mention that Pearce's paper is a pleasant, worthwhile read. to understand our type inference algorithm, only to believe that

• $\st$ is sound and complete
• $\st$ induces a partial order over the universe of FT types
• the universe of FT types, partially ordered by $\st$, is a lattice

Preliminaries

$\Def$ Let $\FT$ be the set of all well-typed FT programs, adhering to the syntax and types stated by the definitions of $\T$ and $\tt t$.

$\Def$ Let $\T^\delta ::= ([\T\to\T^\delta]\T) ~+\!\!|~ \msf{infer}\ n $ denote a type shape that is either a type inference variable distinguished by an integer $n$, or a proper type form where references to proper types may be type shapes.

$\Def$ Let ${\tt t}^\delta ::= [t\to t^\delta, \T\rightarrow\T^\delta] {\tt t}$ denote the syntax of a FT term shape or program shape. In a ${\tt t}^\delta$, type annotations may be type shapes than proper typesIn practice, a parser can admit a term without type annotations entirely, inserting fresh inference variables as needed., and references to other terms maybe term shapes.

$\Def$ Let $\FTS$ be the set of all valid FT program shapes, adhering to the syntax ${\tt t}^\delta$. For simplicity of our conversation, we will demand also that $\FTS$ consists only of program shapes where all type annotations of form $\msf{infer}\ n$ are unique, and furthermore all function and formal names are uniqueFormalizing both these demands is cumbersome and not relevant to our discussion..

$\Def$ Let $\require{cancel}\xFT = \left\{\untypable\right\}$ be the singleton set, symbolically marking an program shape as untypable.

We can describe $\infer$ as a function $\require{cancel}\FTS\to\FT\sqcup\xFT$, yielding either a well-typed FT program or a marker that a program shape is untypableWe could have also defined $\infer$ as a partial function.. Let $\iota_\FT$ and $\iota_\xFT$ denote the canonical projections in the codomain of $\infer$.

Per the FT syntax, we see that type annotations need appear only the formal parameters of a function declaration; hence, formals are also the only place inference variables may appear in a program shape. Our conversation will assume that we are always discussing type annotations on formals.

Inferring single variables

As a first step in approaching this problem, we will examine the simple case of resolving a single inference variable in an otherwise completely-typed program.

$\Def$ Let $x$ be a formal with a inference variable annotation $\msf{infer}\ n$ in a program shape $\PS\in\FTS$. Then $x^?$ denotes the inference variable $\msf{infer}\ n$.

Since we are supposing that all formals and inference variables in program shapes are unique, $x^?$ is unique for the unique variable $x$.

$\Def$ Let $\infvars(\PS\in\FTS)$ denote the set of inference variables $\left\{x_1^?, \ldots, x_n^?\right\}$ attached to all formals $\left\{x_1,\ldots,x_n \right\}$ in $\PS$.

Now, we will describe an algorithm $\infer1\co (x\to\FTS)\to\FTS\sqcup\xFT$ that resolves a program shape $\FTS$ and an inference variable $x^?$ in it to a shape wherein $x^?$ is replaced with the minimal type among all types, if any, satisfying a set of constraints placed on the type of $x$. We recover these constraints from definitions and uses of $x$:

• A definition $x\leftarrow y$ demands $\typeof\ x \supt \typeof\ y$
• A use $y\leftarrow x$ demands $\typeof\ x \subt \typeof\ y$

Bounds

Definition/use constraints on a variable bound that variable's type, a notion we formalize in two definitions below.

Solution sets

Upper and lower boundaries in the universe of types form a (possibly empty) region of types assignable to a constrained variable. We call this region the solution set of an inference variable.

When $x^?$ is solvable in $\PS$, $\LB(x,\PS)$ and $\UB(x,\PS)$ yield a set of proper types $\T$, for which $\st$ is well-defined.

Existence and construction of $\infer1$

Proposition 1 tells us that finding the solution set for a variable completely tells us whether that variable is typable, and gives us valid typings for it in the case that it is. We can now formally define what it means to infer the type of a variable, give conditions on the existence of an inferred type, and give a precise formula for inferring one variable in a program.

Dealing with cycles

At this point, it may seem that $\infer1$ gives us a constructive, sound, and complete algorithm for inferring the minimal type of an inference variable in a program shape. Indeed, we may attempt write a complete $\infer$ algorithm the following way:

$\text{Definition($\infer$: No Cycles)}$

The issue with this algorithm lies on lines 5 and 6: if we have a program shape with inference variables, none of which are solvable, we cannot progress. This means that while $\infer1$ is complete for solvable variables, this definition of $\infer$ is not complete for program shapes!

As an example of a program shape for which the definition above is incomplete, consider

fn f(x: infer 1) = x in
fn g(y: infer 2) = f y in
g (f 1)

we have that $\LB(x, \PS) = \left\{y^?,\int\right\}$ and $\LB(y, \PS) = \left\{x^?\right\}$, so no variable is solvable. But $[x^?\to\int, y^?\to\int]\PS$ yields the following well-typed program

fn f(x: int) = x in
fn g(y: int) = f y in
g (f 1)

Throughout the rest of this section, we describe how to resolve inference variables in the presence of cycles, and prove that our updated method is complete. Our roadmap will be to

• partition inference variables into strongly connected components
• prove that all inference variables in a strongly connected component have a single, unique minimal solution, if any
• show that potential solutions and verification of solutions can be done in two passes
• wrap everything up in a sound, complete, and minimal $\infer$ algorithm

Solution orders

$\Def$ Let $\PS\in\FTS$. The inference dependency graph $\IDG(\PS)$ of $\PS$ is a directed graph where

• the vertices are the inference variables $\infvars(\PS)$

• there is an edge $x^?\to y^?$ exactly when $x^?\in\LB(y, \PS)$

$\text{Definition($\SolOrder$)}.$ Let $\PS\in\FTS$. Let $S_1, \ldots, S_n$ denote the connected components of $\IDG(\PS)$, ordered arbitrarily. Let $C_{i1}, \ldots, C_{in_i}$ denote the strongly connected components of $\S_i$, ordered topologically under condensation.

Then the solution order $\SolOrder(\PS)$ is the strict preorder given by $C_{11} \lt \ldots \lt C_{1n_1}\ldots \lt C_{n1}\ldots \lt C_{nn_n}$.

For example, suppose we have a program shape with the following inference dependency graph:

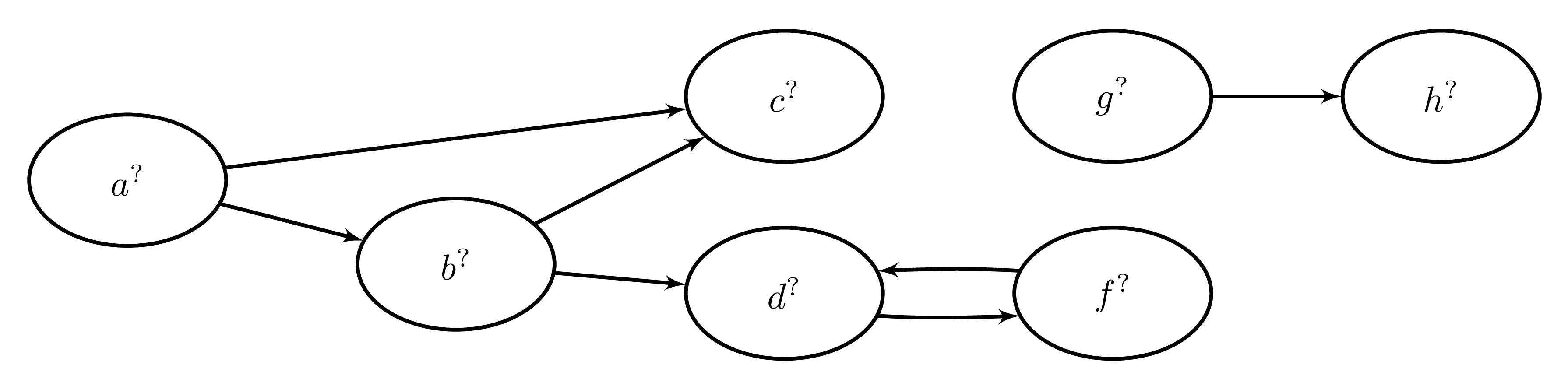
then its connected components and their condensations are given by:

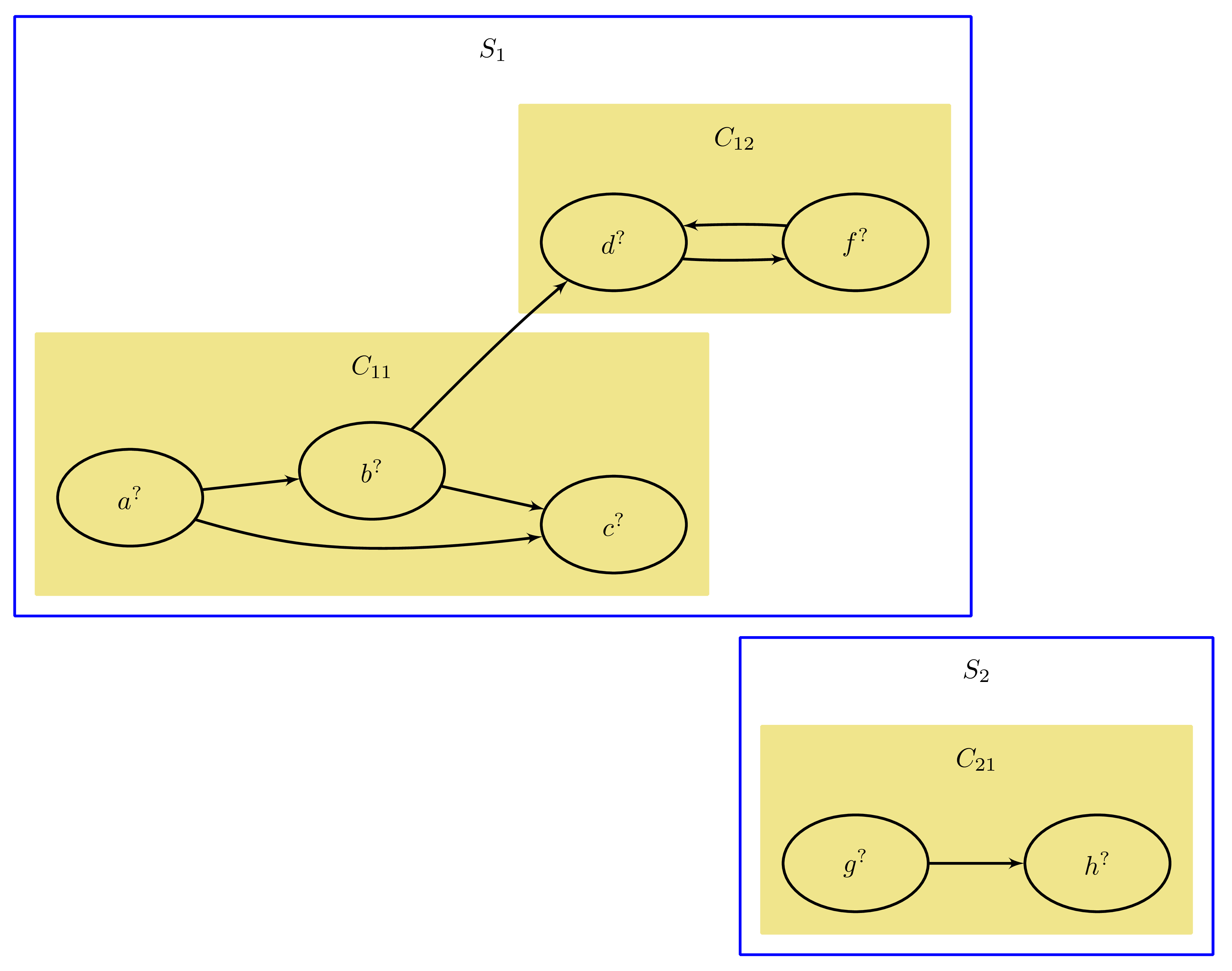
yielding the solution order $C_{11}\lt C_{12}\lt C_{21}$.

Solving for minimal types

An algorithmic account of $\DNF$ and proof of the properties we claim is given in Pearce's paper (Definition 6, Lemmas 4-6).

Putting it all together

$\text{Definition($\infer$)}$ $\infer$ is a function $\FTS\to\FT\sqcup\xFT$, defined below.

Lines 3-6 of the algorithm find potential solutions to the inference variables of $\PS$, and lines 7-10 verify those solutions by comparing them to the (now-resolved) upper bounds of corresponding variables. If verification succeeds, a well-typed program in $\FT$ is returned; otherwise we mark the program shape as uninferrable, and hence untypable.

Note that $\infer$ is well-defined; the only thing that may be of concern is the call to $\Reify(x,P)$, as $\Reify$ is only defined $x\in C$ where $C$ is first-solvable in $P$. But since reification is done in linear solution order $C_1,\ldots,C_n$, once all inference variables in $C_1$ are reified in $P$, $C_2$ becomes first-solvable in $P$.

Conclusion

In this cc, we have presented a sound, complete, and minimal algorithm for type inference of mandatory type annotations in the flow-typing type calculus developed by Pearce, 2012. Our algorithm is constructive and syntax-directed, resolving inference variables from types demanded at definition sites and verifying the legality from types demanded at usage sites.

Our approach to type inference is similar to the classic methods (a la Algorithm W) - collect some constraints and perform unification. Our unification step is more appropriately called resolution, and is more involved than classical unification. In our case, the fact that the FT type universe forms a complete lattice is particularly important.

The finitary nature of the FT calculus complicates the resolution process in the presence of type variable cycles, as an inference variable can incur cyclic constraints that result in a type of infinite depth. Our approach resolves such types to their "closest" legal finitary type by translation to disjunctive normal form, a process that Pearce has noted is exponential in the depth of a type in the worst case (Pearce 2012, section 3.2), and then applying a rewrite procedure whose time and space complexities are linear in variables and type depths but whose rewrite rules are somewhat tricky. The addition of (mutually) recursive types to the FT calculus would trivialize the solution to this issue, though of course would come with its own set of challenges (e.g. type simplification and reformulating $\st$ to be sound and complete).

Takeaways

This is a small problem I toyed with for a couple days, and then took far longer to write up as in this cc. I think it is rather interesting, because type inference in the presence of subtyping is generally considered difficult (though that is usually because of record types and such, not present in FT), and because the FT calculus does not make resolution of certain issues trivial (e.g. cycles cannot be resolved as recursive types).

Designing a compiler with a type inferer out-of-band of the typechecker, as we did here, is also interesting. While the inferer will need to depend a lot on the checker, this decoupling means that multiple inferers for different purposes could be designed. Some ideas include:

• A sound, complete, and minimal inferer, like the one presented here
• An inferer that optimizes for readability of types, avoiding deep nesting
• An inferer that optimizes for a minimal number of unique types
• An inferer that solves for maximal types (principal types in functional languages)