- A definition and an intuition
- Building Kan Extensions
- Absolute Kan Extensions
- Adjoints as Kan Extensions
- Kan Extensions as Monads
- An Application in Homotopy
- Extension Problems
- Resources
There are all kinds of questions mathematicians (and computer scientists,
and programmers, and hobbyists) are interested in asking about relationships
between categories. Functors
tell us how to embed one category in another, natural transformations
tell us how to get from one functor-defined embedding to another, and on we
climb to n-transformations. Adjunctions provide us a notion of weak equivalenceThat is, up
to natural transformations $1_\C\Ra GF$, $FG\Ra1_\D$ which may not be equivalences, but "invertible" in the sense of
the triangle/zig-zag identities. between
categories, and are pervasive as solutions to certain optimization problemsFor instance, there are a tremendous amount of
$\text{Free}\dashv\text{Forgetful}$ adjunctions giving the "best lift" of a simpler object; a canonical example is the
free functor $F\co \Set\to\Set_*$ introducing a freely adjoined pointed element to a set,
and the forgetful functor $U\co \Set_*\to\Set$ that disregards
pointedness. This adjunction induces the Maybe monad, familiar to programmers..
Limits are a "best approximation" of a certain shape by a certain object "from
the right", and colimits are so "from the left"Impressing the idea that adjunctions are weak equivalences, for an indexing category $\J$,
limits are a right adjoint to diagram functors $\C\to\C^\J$, and colimits are
a left adjoint..
Monads give us a notion of closure operations on a category, and inform us of
what information an adjunction preserves. Lawvere theories
are an equivalent mechanism for describing the algebras encoded by a monad.
Another question we may be interested in asking is, what does an extension of a functor along a functor $K\co \C\to\D$ look like? And when no extension exists, how can we best approximate one in a reasonable way? In this cc, I will attempt to outline the answers to these questions and demonstrate some interesting applications, from what I hope is a relatively accessible view. In an effort to cover a lot of material in a short-ish post, we will sometimes gloss over the details of deep ideas. To recover their truth, check the resources at the bottom of this cc; in particular, most of our tour is adapted from Chapter 6 of Reihl. I am not a mathematician, but I am enthusiastic about this, and am writing this for others who feel a similar way.
A definition and an intuition
Suppose you have arrows $f\co X\to Z$, $i\co X\to Y$. We say that $h\co Y\to Z$ is an extension of $f$ along $i$ if $f = h\circ i$.
Now, there is no reason that any arbitrary extension should exist in general. But suppose we are dealing with extensions of functors. In this case, we may be satisfied with an approximation of an extension, where our arrow $h$ is endowed with a natural transformation $f\Ra h\circ i$ or $h\circ i\Ra f$ that is not necessarily yield an equivalence (or worse yet, equality).
It was the interest of Kan to study such approximationsAs far as I can tell, Kan was looking to generalize the construction of certain adjoints for use in homotopy theory. We will discuss one application in this vein later on.. Kan clearly embraced the categorical point of view, for he endowed the extensions of his namesake with a certain universal property as well.
$\Def$ A left Kan extension of a functor $F\co\C\to\E$ along
$K\colon \mathsf C\to\mathsf D$ consists of a functor $\Lan_K F\co \D\to\E$ and
a unit natural transformation $\eta\colon F\Ra\Lan_K F\circ K$
such that for
any other extension pair $(G\co \D\to\E, \gamma\co F\Ra G\circ K)$, there is a
unique $\mu\co \Lan_K F\Ra G$
yielding the factorization $\gamma = \mu K \circ \eta$. This can be visualized
by the pasting
diagramThe way to read the right-hand diagram is as follows.
First, the natural transformation $\eta$ (equivalently, a 2-morphism between morphisms of categories)
takes the arrow $F$ to the composite $\Lan_K F\circ K$. Then, the 2-morphism $\mu K$ takes $\Lan_K F\circ K$
to $G\circ K$. Importantly, $\mu K$ is a whiskering that yields a 2-morphism.
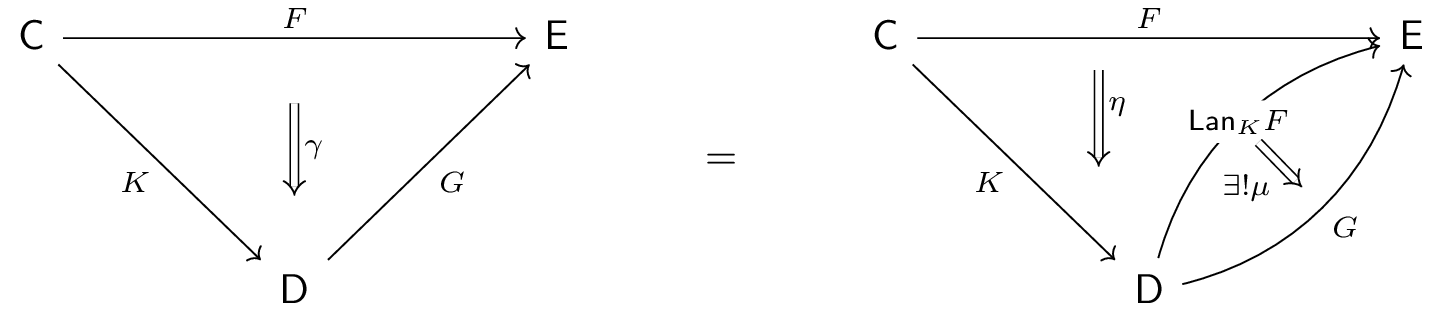
What's left is what's on the right, and indeed there is a dual notion of a
right Kan extension, consisting of a functor $\Ran_K F\co \D\to\E$ and counit natural
transformation $\eps\co \Ran_K F\circ K\Ra F$
such that for any other extension pair $(G\co \D\to\E, \delta\co G\circ K\Ra
F)$, there is a unique $\mu\co G\Ra \Lan_K F$ yielding the factorization $\delta
= \eps\circ\mu K$.
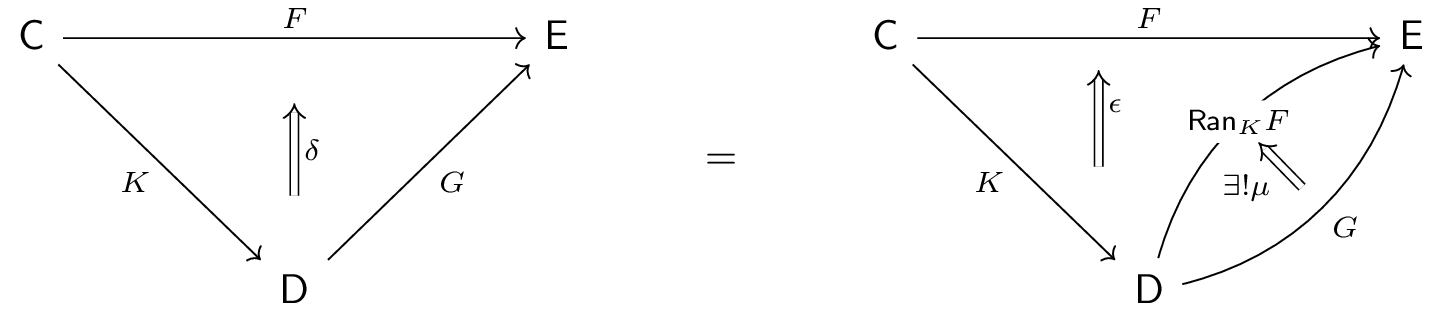
As you may imagine, the universal property of the Kan extension is a very strong tool for use in constructions (like most universal properties are)It may be instructive to describe what category defines the universal property of Kan extensions. Furthermore, the idea that both (co)limits and Kan extensions are a "best approximation" of a particular shape suggests there is a tight relationship between them; how could a (co)limit be represented as a Kan extension? Both of these are extension problems.. Indeed, we will see that the guarantee of these unique arrows drive the way in verification of some interesting propositions and applications.
Kan Extensions as Adjoints
To whet our appetite, let's see how Kan extensions mesh nicely with another powerful concept in category theory - adjoints. Indeed, the universal property of Kan extensions admits a certain class of adjunctions. Fixing the "extension along" functor $K\co \C\to\D$, we can see that when all functors $F\co \C\to\E$ have a left and right Kan extension along $K$, these data assemble into parallel functors $\Lan_K, \Ran_K\co \E^\C\rightrightarrows\E^\D$ that take a functor $\C\to\E$ to its left or right Kan extension $\D\to\E$ along $K$.
$\Thm$ When they exist, $\Lan_K$ and $\Ran_K$ define left and right
adjoints to the pre-composition functor $K^*\co \E^\D\to\E^\C$.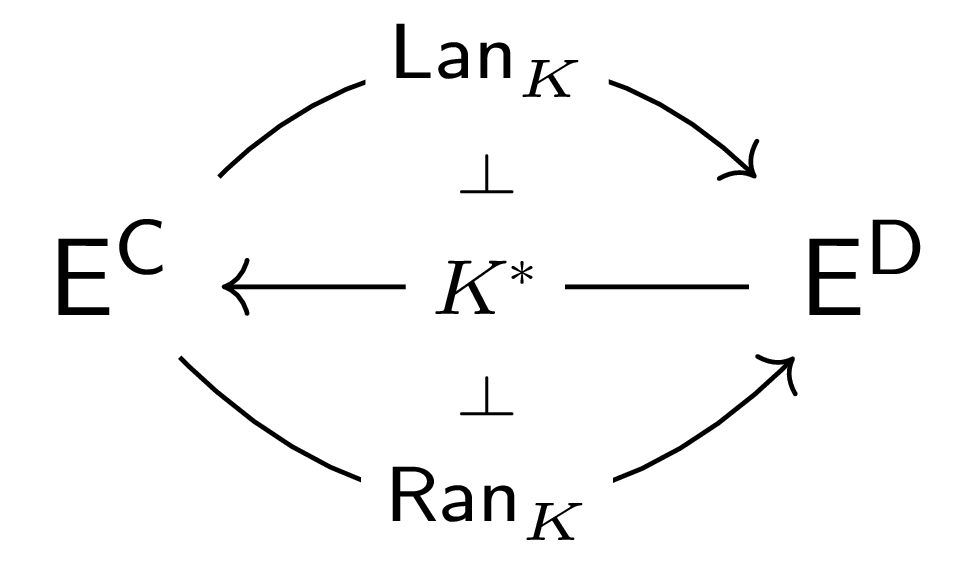
$\Pf$ The universal property of the left Kan extension of $F$ along $K$ demands that for any $G\co\D\to\E$, a natural transformation $F\Ra GK$ corresponds exactly to a natural transformation $\Lan_K F \Ra G$. This correspondence assembles into a natural isomorphism $\E^\D\left(Lan_K F, G\right)\cong \E^\C\left(F, GK\right)$, which is exactly the family of bijections defining the adjunction $\Lan_K\dashv K^*$. That this family of bijections is natural in $F$ and $G$ is relatively straightforward to check; the details are given in Riehl 6.1.5. The argument for $K^*\dashv\Ran_K$ is similar. $\square$
When Extensions are not Kan Extensions
On the other hand, the demand of such a universal property may suggest that Kan extensions are relatively hard to come by, not unlike (co)limits in certain categories. It turns out that the presence of this universal property actually fails to lift extensions to Kan extensions in general.
For example, consider the terminal category $\require{unicode}\1$ consisting of a single object, the discrete category $\bar{\2}$ with two objects, the inclusion functor $\iota\co \1\hookrightarrow\bar\2$, and the constant endofunctor $z\co \bar\2\to\bar\2$ into $0$. By our construction, it is the case that $\iota = z\circ\iota$, so $z$ is a proper extension of $\iota$ along $\iota$; perhaps we would expect that the pair $(z, 1_\iota\co \iota\Ra z\circ\iota)$ yields a left or right Kan extension. But it does neither; consider the pair $(1_\bar{\2}, 1_\iota\co \iota \Ra 1_\bar{\2}\circ \iota)$. If $z$ is a left Kan extension, we need a natural transformation $z\Ra 1_\bar{\2}$, which demands an arrow $0 = z1 \to 1_\bar{\2}1 = 1\in\text{mor}\left(\bar\2\right)$, but no such arrow exists.
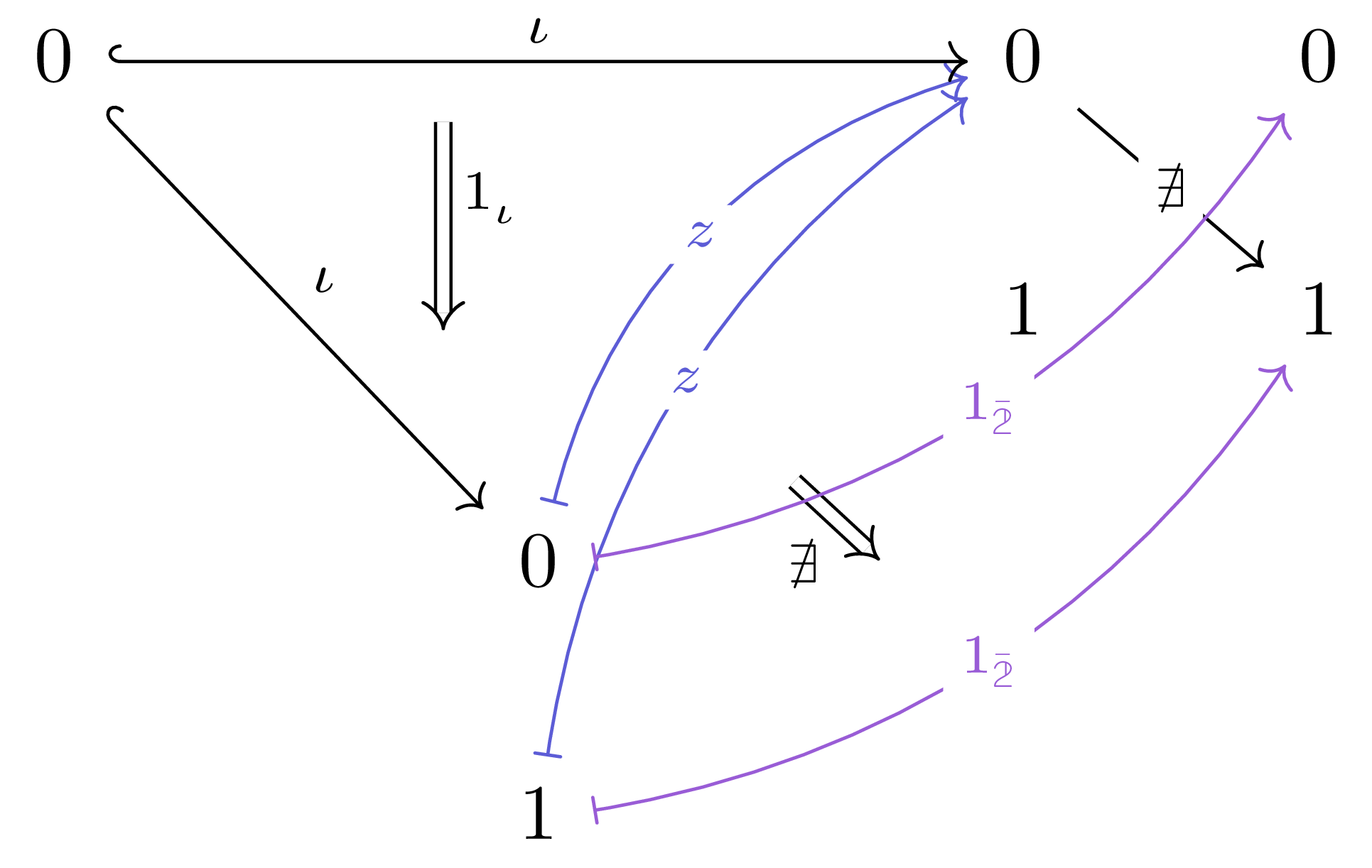
It would be nice to know how to build up certain Kan extensions, just as we know how to build up (co)limits in certain categoriesFor example, we know products and coproducts in $\Set$, which are limits and colimits under a diagram indexed by a discrete category, are exactly the type- and set-theoretic notions of products and disjoint unions.. Category theory never fails to reflect on itself, not the least with great coherence - we will see that certain Kan extensions can be built from certain (co)limits.
Building Kan Extensions
We have already discussed the notion that Kan extensions are a kind-of approximation for a true extension, modulo a natural transformationThe following intuition for the construction of Kan extensions comes from Riehl.. In particular, a left Kan extension of $F\co \C\to\E$ along $K\co \C\to\D$ is the "best" approximation of an extension of $F$ along $K$ "from the left", which is to say up to a natural transformation $\eta\co F\Ra\Lan_KF\circ K$ initial among all natural transformations $F\Ra GK$ via an arrow $\Lan_KF\Ra G$ "from the left". Taking this idea of "approximating from the left" to heart, to define the action of $\Lan_KF$ on an object $d$ we may want to consider the action of $F$ on objects in $\C$ that "approximate" $d$. In the present context, there are two reasonable ways to determine what objects "approximate" $d$. One is to choose those objects $c\in\C$ such that $Kc\cong d$. Another is to choose objects $c\in\C$ whose image under $K$ can "get to" $d$, which is to say there is an arrow $Kc\to d$. Indeed, considering the idea of approximation most universally, the latter feels more appropriate. Such "approximating" arrows $Kc\to d$ are exactly the objects of the comma category $K\downarrow d$, which has a canonical projection functor $\Pi^d\co K\downarrow d\to\C$ that takes an arrow $Kc\to d$ defining an "approximation of $d$ from the left" to the "approximating object" $c$. We can then map each such object via $F$, defining a diagram $K\downarrow d\xrightarrow{\Pi^d}\C\xrightarrow{F}\E$ whose image seemingly provides a number of approximations for the image of $d$ "from the left". How do we collapse these approximations into a single object? Take a colimit!
$\Thm$ Consider $F\co \C\to\E$ and $K\co \C\to\D$. If $\forall d\in\D$ the colimit
of the diagram $F\Pi^d$ exists, these data assemble into a functor $\Lan_K F\co \D\to\E$, and the colimit cones embed the unit $\eta\co F\Ra\Lan_K F\circ K$, such that $\Lan_K F, \eta$ define the left Kan extension of $F$ along $K$.
Dually, if $\forall d\in\D$ the limit
of the diagram $F\Pi_d$ exists, these data assemble into a functor $\Ran_K F\co \D\to\E$, and the limit cones embed the counit $\eps\co \Ran_K F\circ K\Ra F$, such that $\Ran_K F, \eps$ define the right Kan extension of $F$ along $K$.
$\text{Sketch}.$ We will describe exactly what $\Lan_KF\co \D\to\E$ and the unit $\eta\co F\Ra\Lan_KF\circ K$ of the left Kan extension look like. First of all, let us denote the cocone of each colimit $\Lan_KF(d)$ as $\lam^d\co F\Pi^d\Ra\Lan_KF(d)$. Now, taking a morphism $g\co d\to d'\in \D$, we can define a cocone $\bar\lam^{d'}\co F\Pi^d\Ra\Lan_KF(d')$ whose components are given by $\bar\lam^{d'}_{f\co Kc\to d} := \lam^{d'}_{gf\co Kc\to d'}$. By the universal property of the colimit $\Lan_KF(d)$, this induces a unique arrow $\Lan_KF(g)\co \Lan_KF(d)\to\Lan_KF(d')$ factoring $\bar\lam^{d'}$ through $\lam^d$.
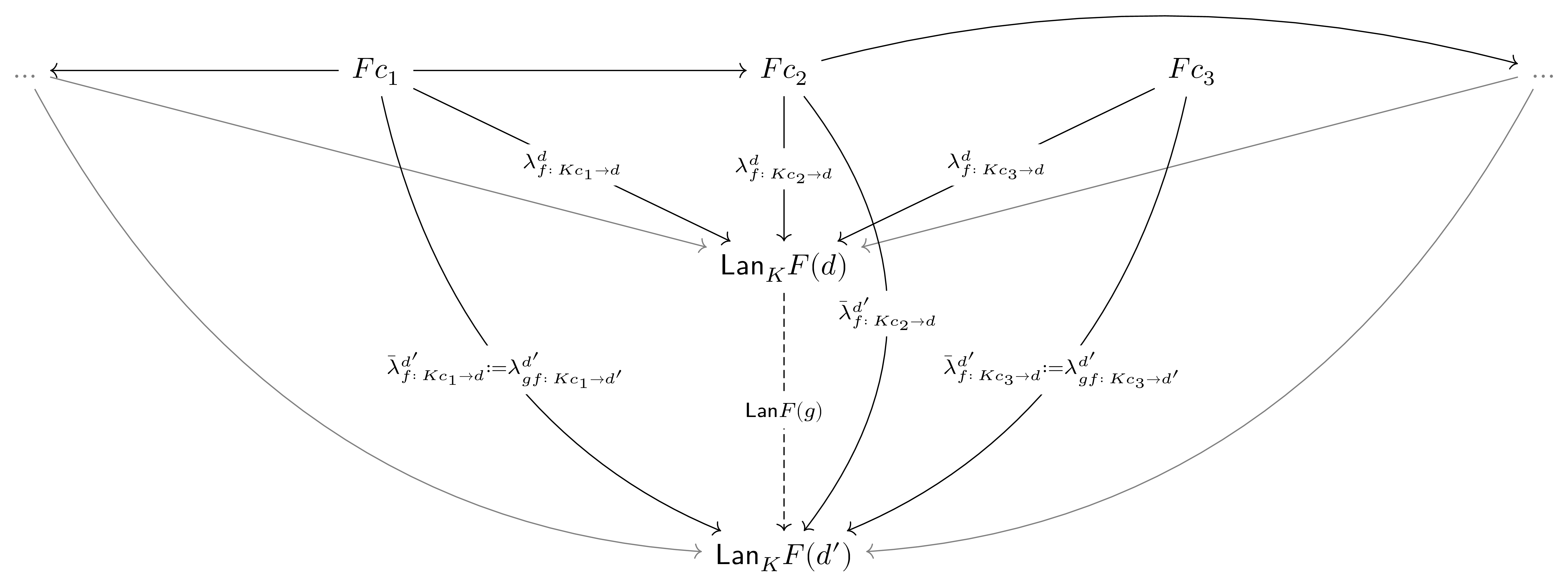
Functoriality of $\Lan_KF$ follows from the uniqueness of this arrowIf you have not verified a "functoriality-by-uniqueness" proof before, here is a good chance to do so.. We recover the unit $\eta\co F\Ra\Lan_KF\circ K$ by defining
The naturality of $\eta$ is straightforward to verify using the action of $\Lan_KF$ on morphisms, while proof of the universal property of the left Kan extension is given by Riehl 6.2.1. $\diamond$
An example: Continuous functions in the reals
$\text{Problem.}$ Suppose we are given some subset $\S$ of the realsGood options are $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, or $\R$ itself.. When does a monotonic function $f\co (\S, \le)\to(\R, \le)$ have both a left and right Kan extension along the inclusion $\iota\co \S\hookrightarrow\R$, and when are these extensions equal?
$\text{Solution.}$ Applying the colimit formula for left Kan extensions, we see that $\Lan_\iota f\co \R\to\R$ exists when $\forall r\in\R$ the diagram $\iota\downarrow r\xrightarrow{\Pi^r}\S\xrightarrow{f}\R$ admits a colimit. This diagram is indexed by arrows $\iota(n\in\S)\to r$, and the image of each such arrow is $f(n)\in\R$; that is to say, if the colimit of this diagram exists, it is the supremumAll colimits in a poset category are suprema of bounded subsets. of $\left\{f(n) ~|~ n\le r\right\}$. Indeed this colimit exists, for $\left\{f(n) ~|~ n\le r\right\}$ is bounded above in $\R$, and all non-empty sets bounded above in $\R$ have a supremum. Denoting the colimit cone at $r$ $\lam^r\co (\iota\downarrow r\xrightarrow{\Pi^r}\S\xrightarrow{f}\R)\Ra \sup\left\{f(n)~|~ n\le r\right\}$, we have that the unit $\eta\co f\Ra \Lan_\iota f\circ \iota$ of the left Kan extension is given by the components $\eta_n = \lambda_{1_{\iota n}}^{\iota n}$, which in particular demands the relation $f(n)\le \Lan_\iota f(n)$, hence it must be that $f(n)\le\sup\left\{f(q) ~|~ q\le n\right\}$ $\forall n\in\S$. But $f$ is monotonic, so this strictly implies $f(n)=\sup\left\{f(q) ~|~ q\le n\right\}$. That is to say, $f$ admits a left Kan extension along $\S\hookrightarrow\R$ when $f$ is continuous on the left.
Applying the dual limit formula for right Kan extensions, we find that a right Kan extension of $f$ along $\S\hookrightarrow\R$ demands $f(n)=\inf\left\{f(q) ~|~ q\ge n\right\}$ $\forall n\in\S$, which is to say that $f$ is continuous on the right.
Putting this together, $\Lan_{\iota}f = \Ran_{\iota}f$ exactly when $f$ is continuous.Anna Marie Bohmann says this is probably a terrible way to first introduce the notion of continuous functions. But I say, this is exactly the viewpoint the nLab would want us to embrace. I'll leave you to decide whether a graduate-level course on category theory should be part of a high school math curriculum. $\square$
These demands make intuitive sense as well. A left Kan extension of $f$ along the inclusion into $\R$ is in some sense the "best approximation" of $f$ in $\R$ "from the left", so it seems natural that $f$ should be continuous at least on the left for this to make any sense.
Absolute Kan Extensions
Before we get to more fun applications, we have to introduce some auxiliary definitions relating to Kan extensions. The first is analogous the preservation of (co)limits by certain functors.
$\Def$ A functor $L\co \E\to\J$ preserves left Kan extensions if, for all left Kan extensions $(\Lan_K F, \eta)$ of $F\co \C\to\E$ along $K\co \C\to\D$, $(L\Lan_K F, L\eta)$ is a left Kan extension of $LF$ along $K$.
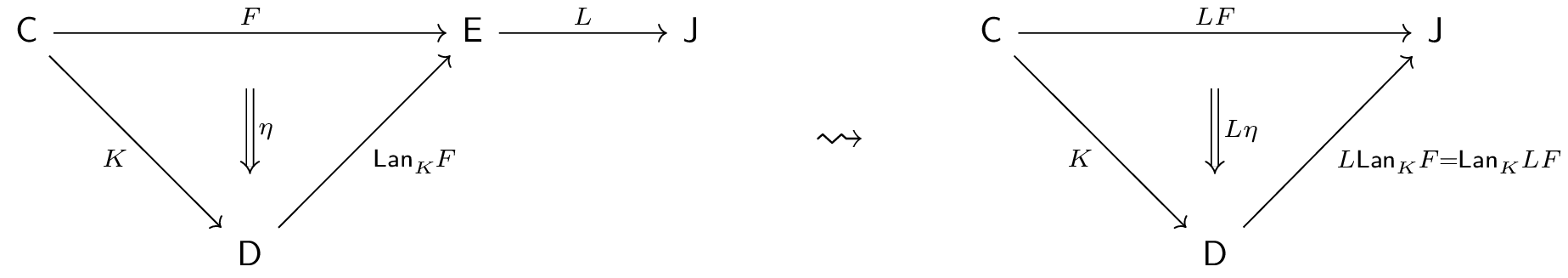
The notion of preservation for right Kan extensions is similar.
A natural to question to ask is whether adjoints preserve Kan extensions, like they preserve (co)limits. Indeed
$\Thm$ Left adjoints preserve left Kan extensions. Dually, right adjoints preserve right Kan extensions.
$\text{Sketch}.$ Hint: Use the natural isomorphism defining an adjunction and the universal property of Kan extensions to construct a chain of natural isomorphisms demonstrating that $(L\Lan_K F, L\eta)$ is a left Kan extension of $LF$ along $K$. For details, or a visual proof via pasting diagrams, see Riehl 6.3.2. $\diamond$
There is a certain class of Kan extensions that turn out to be surprisingly useful, and whose definition depends on the notion of preservation.
$\Def$ A right Kan extension $\Ran_K F\co \D\to\E$ is pointwise if it is preserved by representable functors $\E(e, -)$ $\forall e\in\E$.
The definition of a pointwise left Kan extension is dual, but the arrows of 2-morphisms are reversed rather than the arrows of 1-morphisms. It turns out that a Kan extension is pointwise exactly when it can be computed by the (co)limit formula given earlier (Riehl 6.3.6, 6.3.7).
Here is an interesting fact regarding pointwise Kan extensions.
$\Thm$ If $\E$ is small and admits all small copowersIterated coproducts of a single object, all right Kan extensions with codomain $\E$ are pointwise. Dually, if $\E$ is small and admits all small powers, all left Kan extensions with codomain $\E$ are pointwise.
$\Pf$ When $\E$ admits all copowers, a functor $\E\to\Set$ is representable iff it has a left adjoint. Hence, all representable functors $\E(e,-)$ are right adjoints, and right adjoints preserve right Kan extensions. $\square$
Preservation by representables may seem somewhat arbitrary, and indeed we may want to ask if there are Kan extensions that are preserved by everything. Certainly these are even more rare, but they do exist.
$\Def$ A Kan extension is absolute if it is preserved by all functors.
At this point, these definitions may seem well and good but unsatisfying. Where do Kan extensions arise, and what are they good for? To answer this, perhaps it is best to tie the knot with other concepts in Category Theory and see how Kan extensions provide a categorical point-of-view in other mathematics. As a first application, let us further explore the relationship between adjunctions and Kan extensions.
Adjoints as Kan Extensions
We have seen that Kan extensions give rise to a certain class of adjunctions ($\Lan_K\dashv K^*\dashv\Ran_K$). Do adjunctions give rise to Kan extensions? Certainly!
$\Thm$ If $F\dashv G$ is an adjunction with unit $\eta$ and counit $\eps$, $(G,\eta)$ defines a left Kan extension of the identity along $F$, and $(F,\eps)$ defines a right Kan extension of the identity along $G$. Furthermore, both Kan extensions are absolute.

$\Pf$ An adjunction $F\dashv G$ gives rise to an adjunction between their precomposition functors. Specifically in the case of precomposing functors with codomain $\C$, there is an adjunction
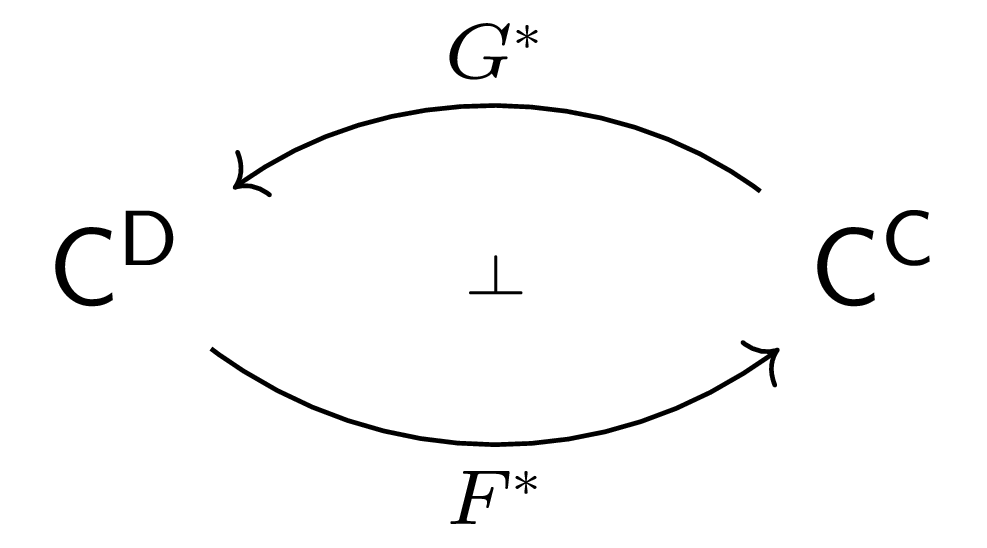
But $\Lan_F\dashv F^*$, so $G^*\cong \Lan_F$ because adjoints are unique up to unique isomorphism. After checking some details (Riehl 6.5.2, 4.4.6), this tell us that the left Kan extension of $1_\mathsf{C}$ along $F$ is given by $(G, \eta)$. To show that this Kan extension is absolute, consider another functor $L\co \C\to\E$ and let $(H\co \D\to\E, \gamma\co L\Ra HF)$ be an extension of $L$ along $F$. We claim that this factors through the preserved left Kan extension $(LG, L\eta)$ of $L$ along $F$ via $H\eta\circ\gamma G$. A series of pasting diagram rewrites, given by the naturality of $\gamma$ and the zig-zag/triangle identity of the adjunction $F\dashv G$ verifies this.
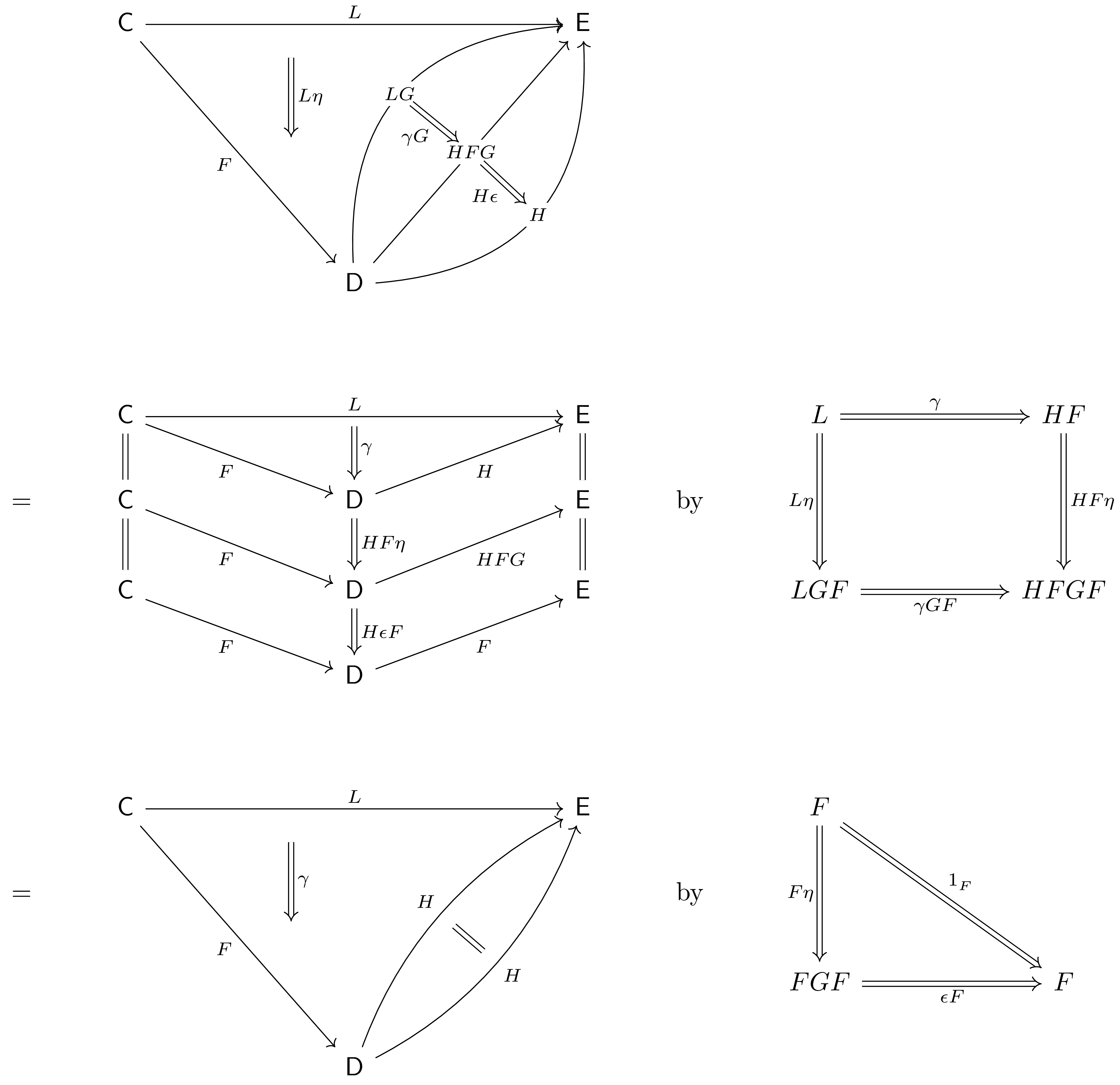
To see that this factorization is unique, suppose there is a $\mu\co LG\Ra H$ such that $\gamma = \mu F\circ L\eta$. Then by this definition, the naturality of $\mu$, and the zig-zag/triangle identity of the adjunction $F\dashv G$,

we see that the factorization $\gamma = \mu F\circ L\eta$ is equally $\gamma = (H\eta\circ\gamma G)F\circ L\eta$. By uniqueness, this demands $\mu = H\eta\circ\gamma G$. $\square$
Naturally, adjunctions may also be recovered from Kan extensions of identities.
$\Thm$ If $(G, \eta\co 1_\C\Ra GF)$ is a left Kan extension of $1_\C$ along $F$ and furthermore $F$ preserves this Kan extension, $F\dashv G$ is an adjunction with unit $\eta$.
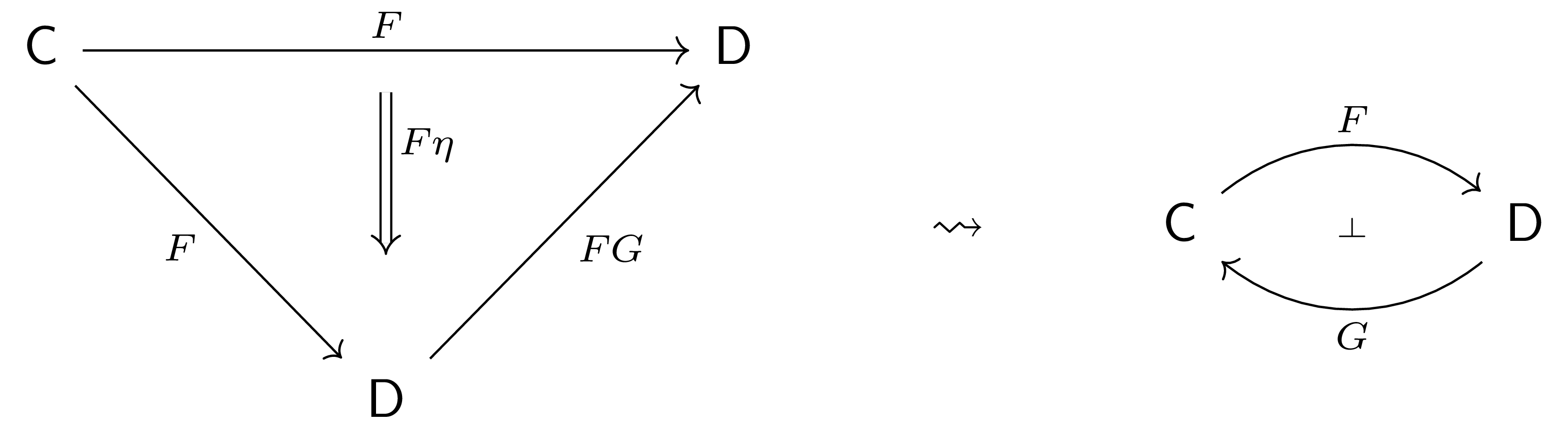
$\Pf$ If the left Kan extension $(G,\eta)$ is preserved by $F$, $(FG, F\eta\co F\Ra FGF)$ is a left Kan extension of $F$ along itself. Taking the extension pair $(1_\D, 1_F)$, the universal property of the left Kan extension demands a unique $\eps\co FG\Ra 1_\D$ such that $1_F = \eps F\circ F\eta$.
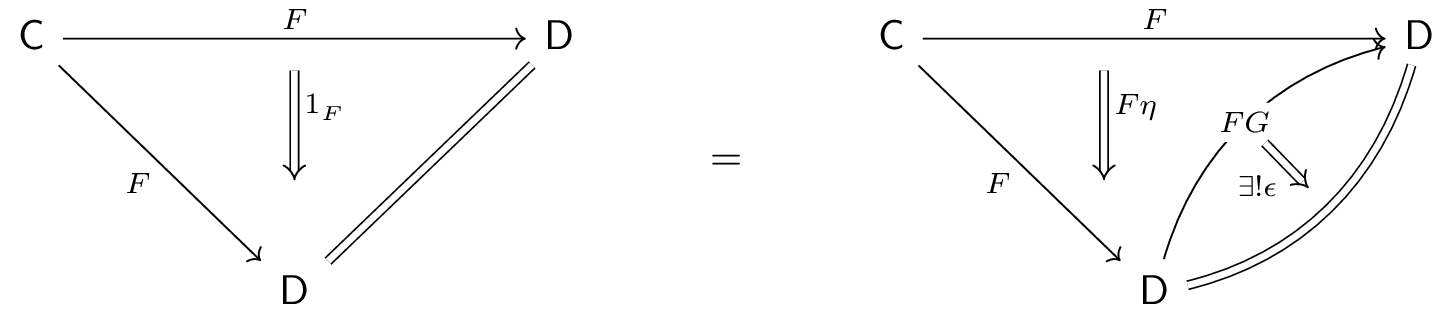
Taking $\eps$ to be the counit of the proposed adjunction, this demonstrates one zig-zag/triangle identity. To see the other, consider the extension pair $(G,\eta)$ of $1_\C$ along $F$; clearly, this factors through the left Kan extension $(G,\eta)$ (itself) via the identity. Rewriting the factorization pasting diagram using the already-demonstrated identity $1_F = \eps F\circ F\eta$,
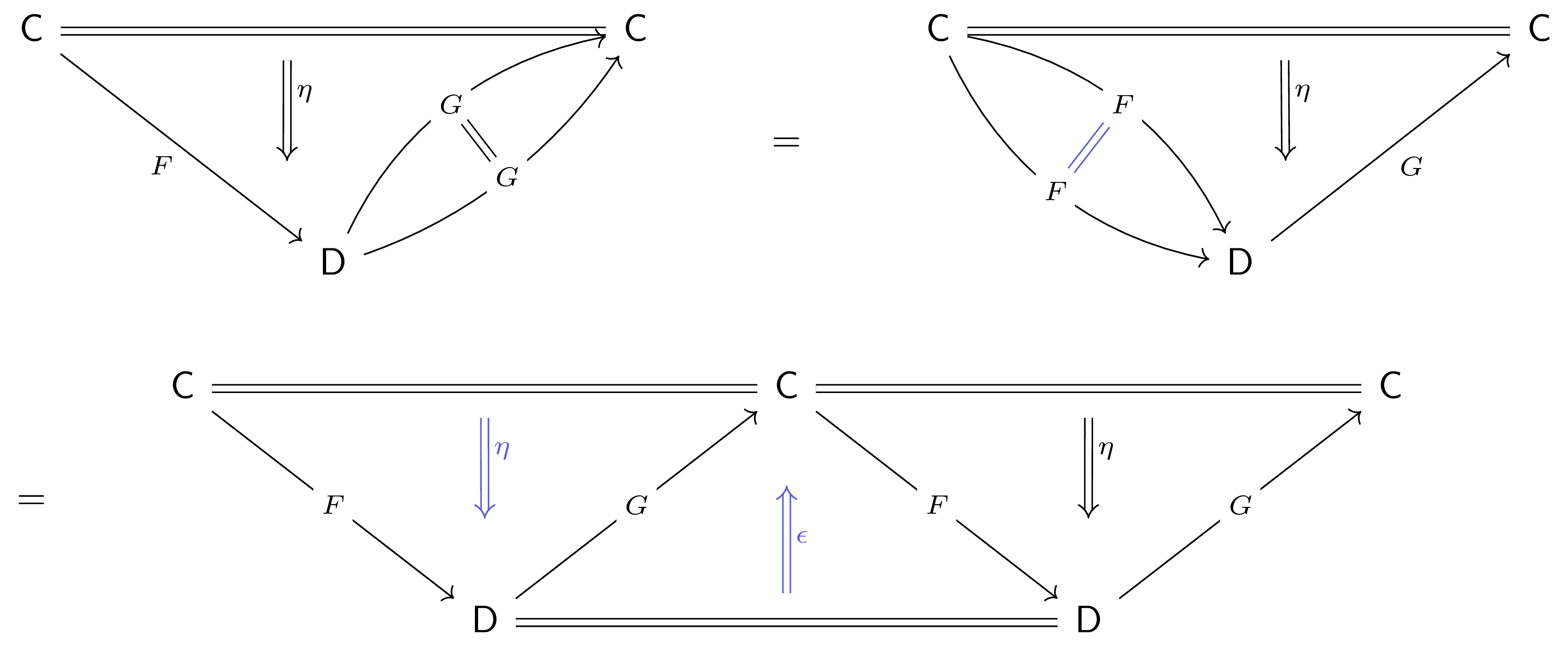
which communicates that the $(G,\eta)$ is factored through itself by $G\eps\circ\eta G$. By uniqueness of the universal property of the left Kan extension, this demands $1_G = G\eps\circ\eta G$. $\square$
Where there is an adjunction there is a monad, so we can keep the conversation going - when can we recover monads from Kan extensions?
Kan Extensions as Monads
It turns out the demands to find a canonical monad from a Kan extension are looser than those of finding an adjunction in the manner presented above. In particular, there is no requirement of preservation.
$\Thm$ When the right Kan extension of $G\co \D\to\C$ along itself exists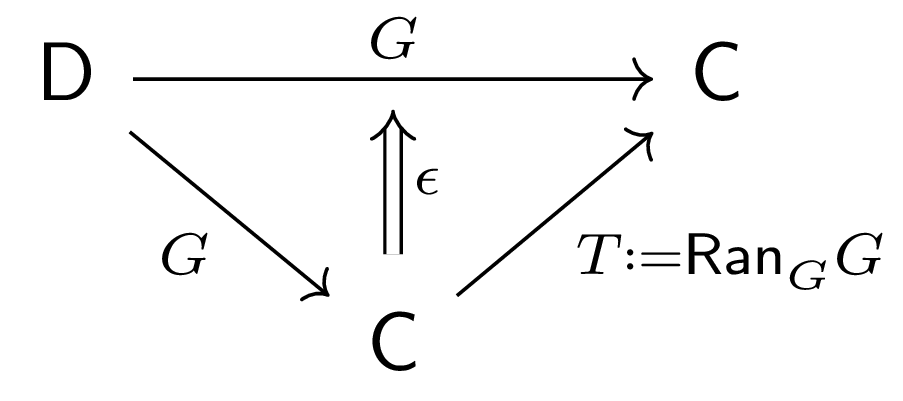
,
this Kan extension induces a monad over $\C$, termed the codensityWe say
a functor is dense if its left Kan extension along itself is the identity;
dually, it is codense if its right Kan extension along itself is the identity. Applying the
colimit formula for left Kan extensions, this says that given a dense functor $F\co\mathsf{S}\to\C$
where $\mathsf{S}$ is a subcategory of $\C$, all objects in $\C$ are colimits of certain
diagrams from $\mathsf{S}$. There is much more to this topic outside the scope of this
post, including relationships to the (co)Yoneda Lemma; the nLab provides a good
overview. monad of
$G$.
In particular, defining $T:=\Ran_G G$, $\eps\co TG\Ra G$ as the counit of the right Kan extension, $\eta\co 1_C\Ra T$ as the unique
factorization of $(1_\C, 1_G)$ through $(T,\eps)$, and $\mu\co T^2\Ra T$ as the
unique factorization of $(T^2, \eps\circ T\eps)$ through $(T,\eps)$, the triple
$(T, \eta, \mu)$ defines a monad on $C$.
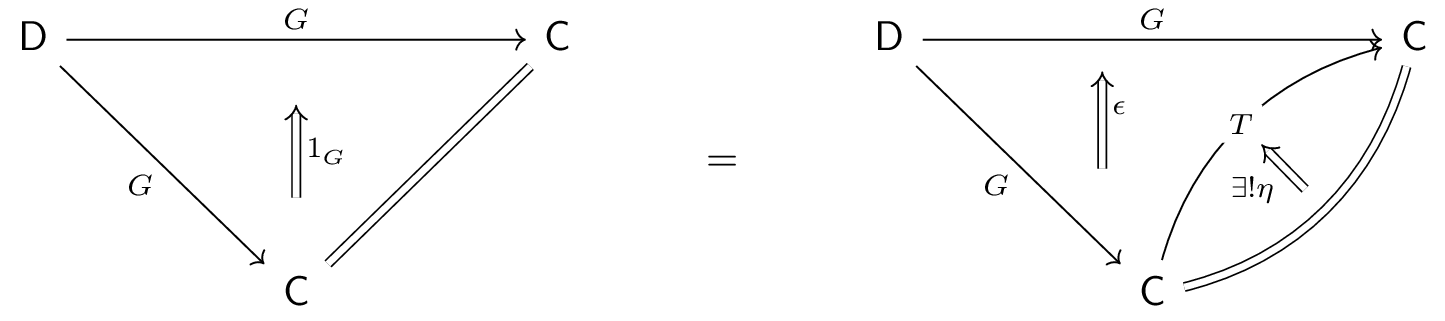
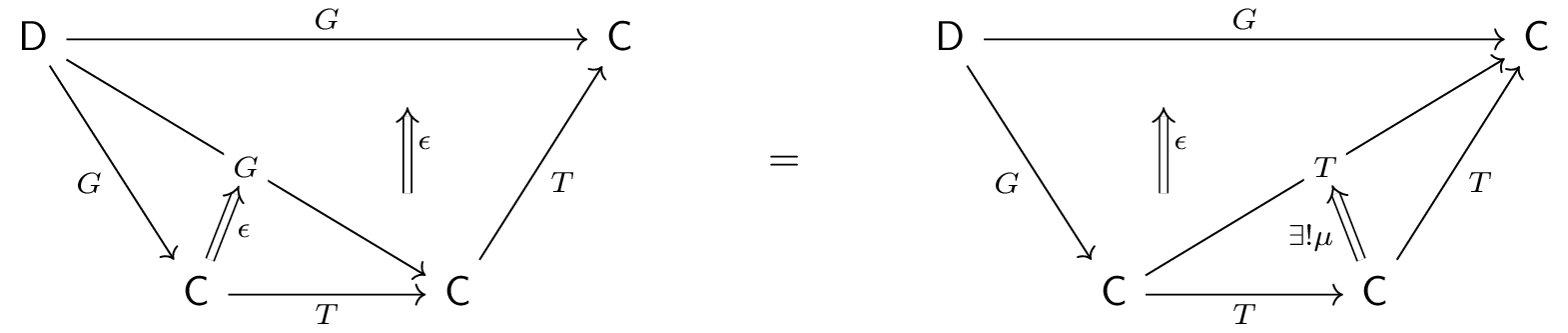
$\Pf$ First, we show the monadic commutativity condition $\mu\circ\mu T =
\mu\circ T\mu$.
Consider the extension pair $(T^3, \eps\circ T\eps\circ T^2\eps\co T^3G\Ra G)$.
Applying the factorization defining $\mu$ two different ways,
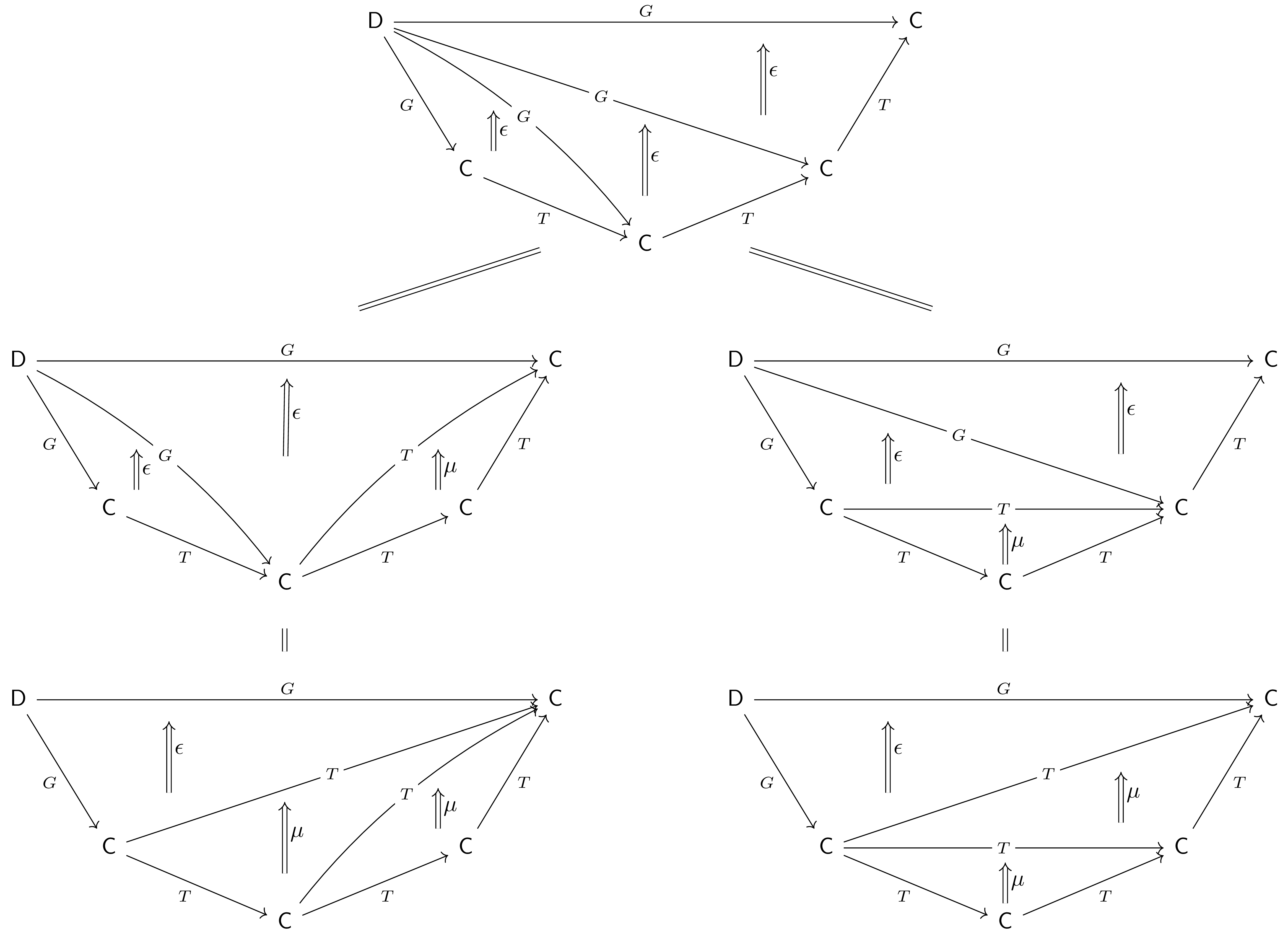
we see that both $\mu\circ\mu T$ (above left) and $\mu\circ T\mu$ (above right) factor $\eps\circ T\eps\circ T^2\eps$ through the right Kan extension. Uniqueness of this factorization demands $\mu\circ\mu T = \mu\circ T\mu$.
For the monadic commutativity condition $\mu\circ\eta T = 1_T = \mu\circ T\eta$
,
consider the extension pair $(T,\eps)$, which factors uniquely through itself
via $1_T$. Applying the factorizations defining $\eta$ and $\mu$ two different
ways,
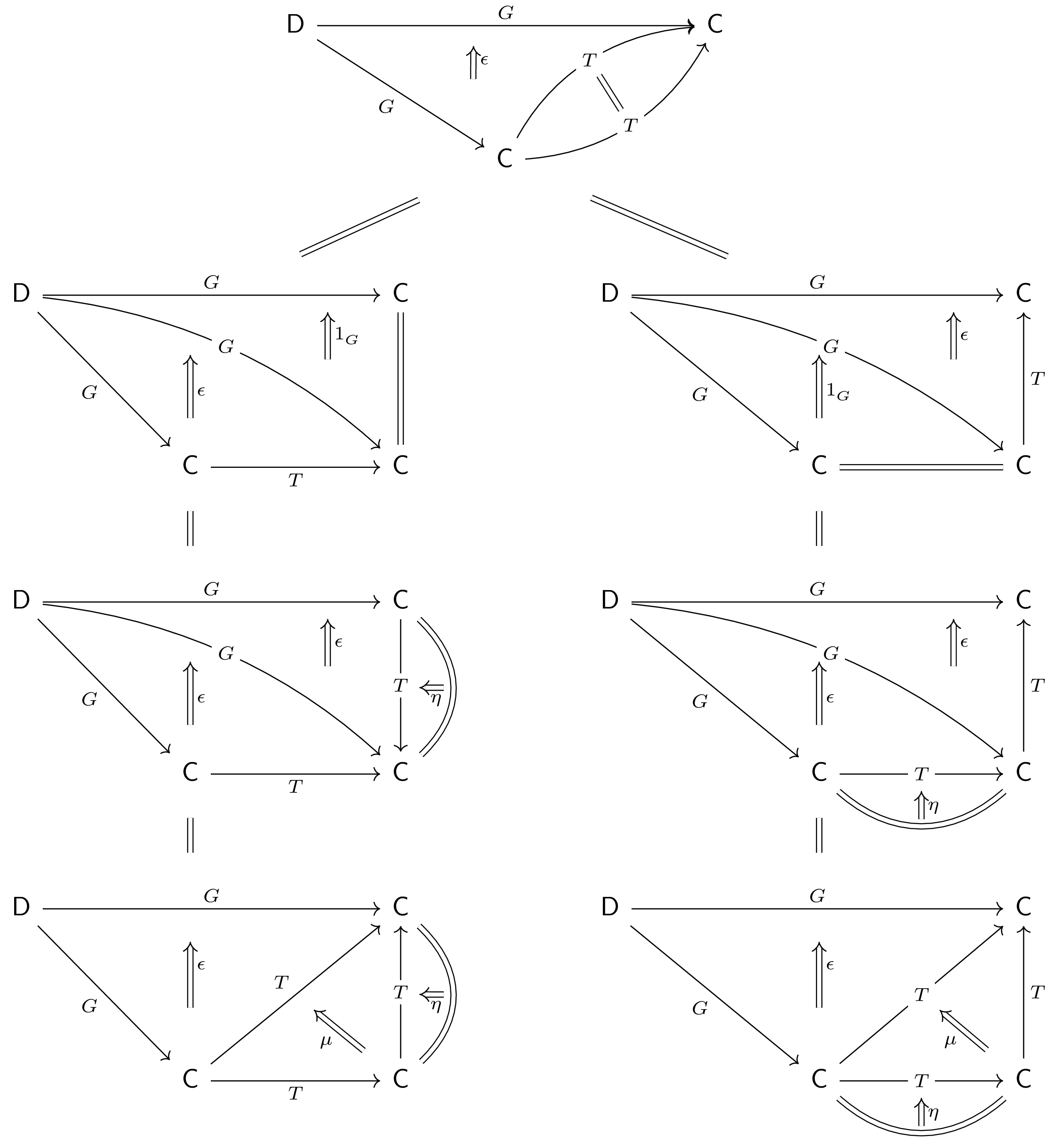
we see that both $\mu\circ\eta T$ (above left) and $\mu\circ T\eta$ (above right) factor $\eps$ through itself. Again, uniqueness of this factorization demands $\mu\circ\eta T = \mu\circ T\eta$, and furthermore both composites must also equal $1_T$. $\square$
Not only are codensity monads canonical, they are canonically canonical.
$\Thm$ If $G$ admits a left adjoint $F$, then $G$ admits a codensity monad, and furthermore the codensity monad of $G$ is the canonical monad $(GF, \eta, G\epsilon F)$ induced by $F\dashv G$ where $\eta$, $\epsilon$ are the unit and counit of the adjunction, respectively.
$\Pf$ When $F\dashv G$, $(F, \eta)$ is a right Kan extension of $1_\D$ along $G$.
Right adjoints preserve right Kan extensions, so $(GF, G\eta)$ is a right Kan
extension of $G$ along itself, which is to say the codensity monad of $G$ is
given by $GF$. This is exactly the endofunctor of the canonical monad induced by
$F\dashv G$. $G\eps \circ \eta G = 1_G$ by one triangle identity, so $\eta$ is
the multiplication of the condensity monad. By the naturality of $G\eps$, $G\eps\circ GFG\eps = G\eps\circ
G\eps FG$
, so $G\eps F$ is the
multiplication of the codensity monad. $\square$
An Application in Homotopy
To finish off this tour, let's see a role Kan extensions play in the field they first arose from. To start, we need to define a weak notion of isomorphism.
$\Def$ A class of morphisms $M$ in a category $\C$ satisfies the 2-of-6 property if for any composable triple $f,g,h\in \text{mor}(\C)$, $hg, gf\in M\implies f,g,h,hgf\in M$.
$\Def$ For a category $\C$, a class of weak equivalences is a class of morphisms $W\subseteq \text{mor}(\C)$ containing all the identities and satisfying the 2-of-6 property.
It is straightforward to show that all isomorphisms are weak equivalences. Now, here's where the homotopy comes in.
$\Def$ A category equipped with a class of weak equivalences is a homotopical category.
$\Def$ A functor is homotopical if it is between homotopical categories, and it preserves weak equivalences.
It is similarly straightforward to show that an endofunctor $F$ on a homotopical category $\C$ is a homotopical functor if it is equipped with a natural weak equivalenceThat is, a natural transformation whose components are all weak equivalences. to ($\require{extpfeil}\Newextarrow{\xRightarrow}{5,5}{0x21D2}F\xRightarrow{\sim}1_\C$) or from ($1_\C\xRightarrow{\sim}F$) the identity.
Now suppose that $\C$ is a homotopical category, and there is some functor $F\co \C\to\D$ taking the weak equivalences to isomorphisms. It turns out that such functors arise frequently in homotopy, and so it may be natural to ask what it means to have an initial or final object in the category of such functors. The final object is not that interestingwhat is it?, but the universal property of the initial object certainly is.
$\Def$ For any homotopical category $\C$, there is a homotopy category $\HoC$ and a universal localization functor $Q_\C\co \C\to\HoC$ that is initial in the category of functors that takes weak equivalences in $\C$ to isomorphisms.
What a homotopy category looks like doesn't matter too much for us, but a good intuition for its shape is given by the homotopical notion that many arrows can be seen as equivalent or invertible up to homotopy. For more details, Wikipedia has a nice construction, as does Gabriel and Zisman, 67.
Now suppose we have a homotopical functor $\C\to\D$. We may be interested in the "localization" of this functor; that is, does this functor induce a functor $\HoC\to\HoD$ between homotopy categories, and if so, what does such a functor look like? Maybe you already see where this is going - we can phrase these questions as extension problems.
$\Def$ Let $F\co \C\to\D$ be a homotopical functor. When it exists, the right Kan extension $\dL F:=\Ran_{Q_\C}Q_\D F$ of $Q_\D F$ along $Q_\C$ defines the total left derived functor of $F$.
Dually, when it exists, the left Kan extension $\dR F:=\Lan_{Q_\C}Q_\D F$ defines the total right derived functor of $F$.
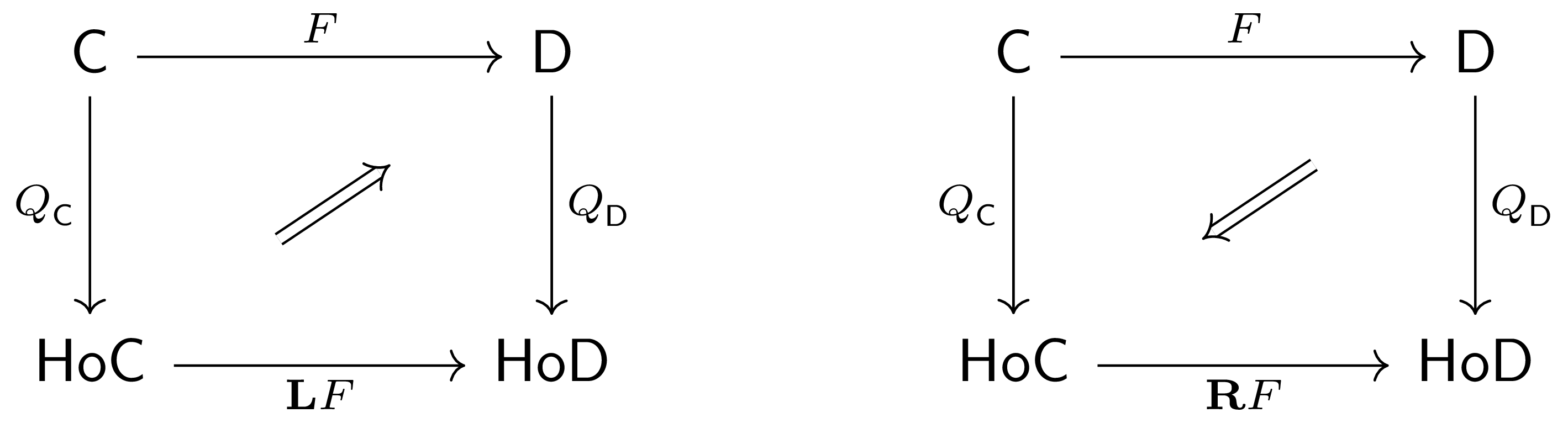
Since total derived functors are in some sense an approximation of a homotopical functor, it is reasonable to ask if a total derived functor observes the same functorial properties as the functor it was derived from. More generally, we could pose this question for any Kan extension; indeed in general there is no reason this should be true, but Maltsiniotis has found a preservation in the former case.
$\Thm$ Let $F\co \C\leftrightarrows\D \co G$ be homotopical functors where $F\dashv G$. Suppose furthermore that $F$ has a total left derived functor $\dL F$ and $G$ has a total right derived functor $\dR G$, where both total derived functors are absolute Kan extensions. Then there is an adjunction $\dL F\dashv\dR G$.
$\Pf$ Let $Q_\C\co \C\to\HoC$ and $Q_\D\co \D\to\HoD$ be the appropriate
localization functors, $(\dL F, \phi)$ be the absolute right Kan extension of $Q_\D F$
along $Q_\C$ constituting the total left derived functor of $F$, and $(\dR G,
\psi)$ be the absolute left Kan extension of $Q_\C G$ along $Q_\D$ constituting the total
right derived functor of $G$.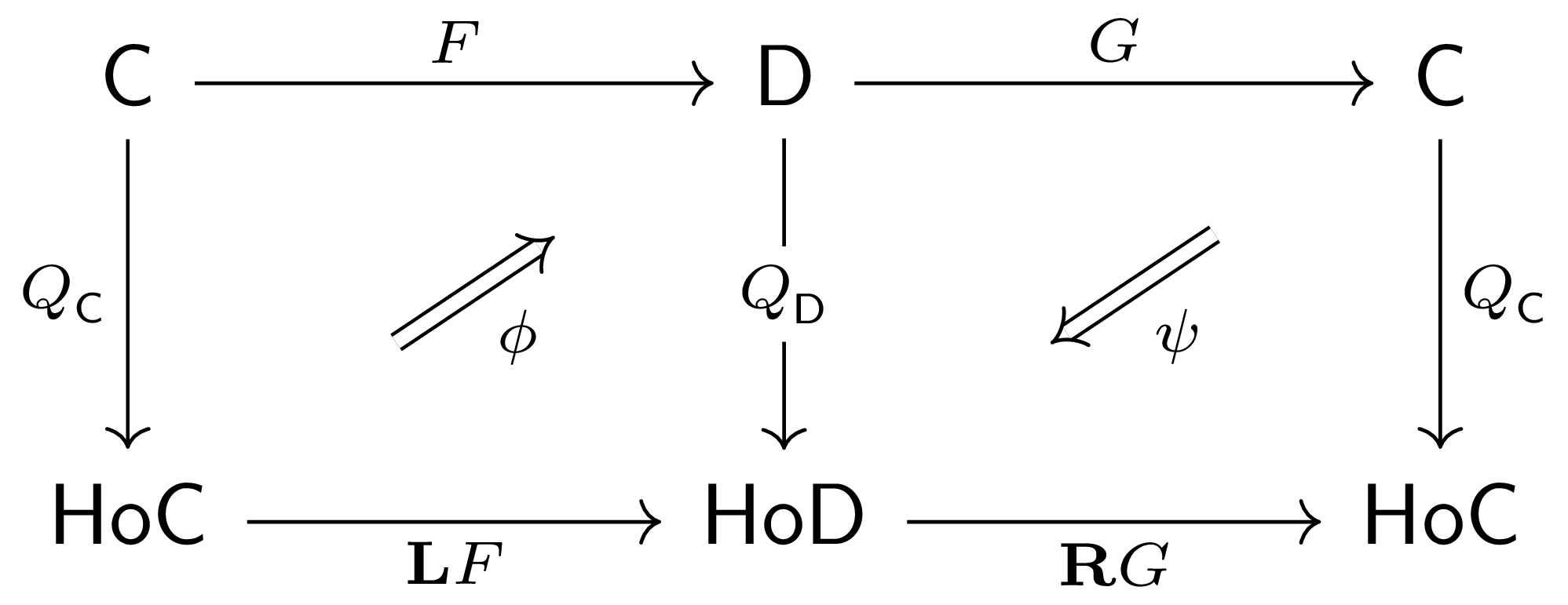
Furthermore, let $\bar\eta$ and $\bar\eps$ be the
unit and counit of the adjunction $F\dashv G$, respectively.
Consider the extension pair $\displaystyle\left(1_\HoC, Q_\C\xRightarrow{Q_\C\bar\eta}Q_\C GF\xRightarrow{\psi F}\dR GQ_\D F\right)$. Since $(\dL F, \phi)$ is an absolute right Kan extension, $(\dR G\dL F, \dR G\phi)$ is a right Kan extension of $\dR GQ_\D F$ along $Q_\C$. By the universal property of this Kan extension, $\exists! \eta\co 1_\HoC\Ra\dR G\dL F$ such that $\dR G\phi\circ\eta Q_\C = \psi F\circ Q_\C\bar\eta$.

Consider the extension pair $\displaystyle\left(1_\HoD, \dL FQ_\C G\xRightarrow{\phi G}Q_\D FG\xRightarrow{Q_\D\bar\eps}Q_\D\right)$. $(\dL F\dR G, \dL F\psi)$ is a left Kan extension of $\dL FQ_\C G$ along $Q_\D$, and by the universal property of this Kan extension $\exists! \eps\co \dL F\dR G\Ra 1_\HoD$ such that $\eps Q_\D\circ\dL F\psi = Q_\D\bar\eps\circ\phi G$.

We claim that $\eta$, $\eps$ form the unit and counit of an adjunction $\dL
F\dashv\dR G$. To verify the zig-zag identity $\eps \dL F\circ\dL F\eta =
1_{\dL F}$, consider that $1_{\dL F}$ is the unique 2-morphism factoring the
right Kan extension $(\dL F, \phi)$ through itself; that is, $\phi = \phi\circ
1_{\dL F}Q_\C$. But also,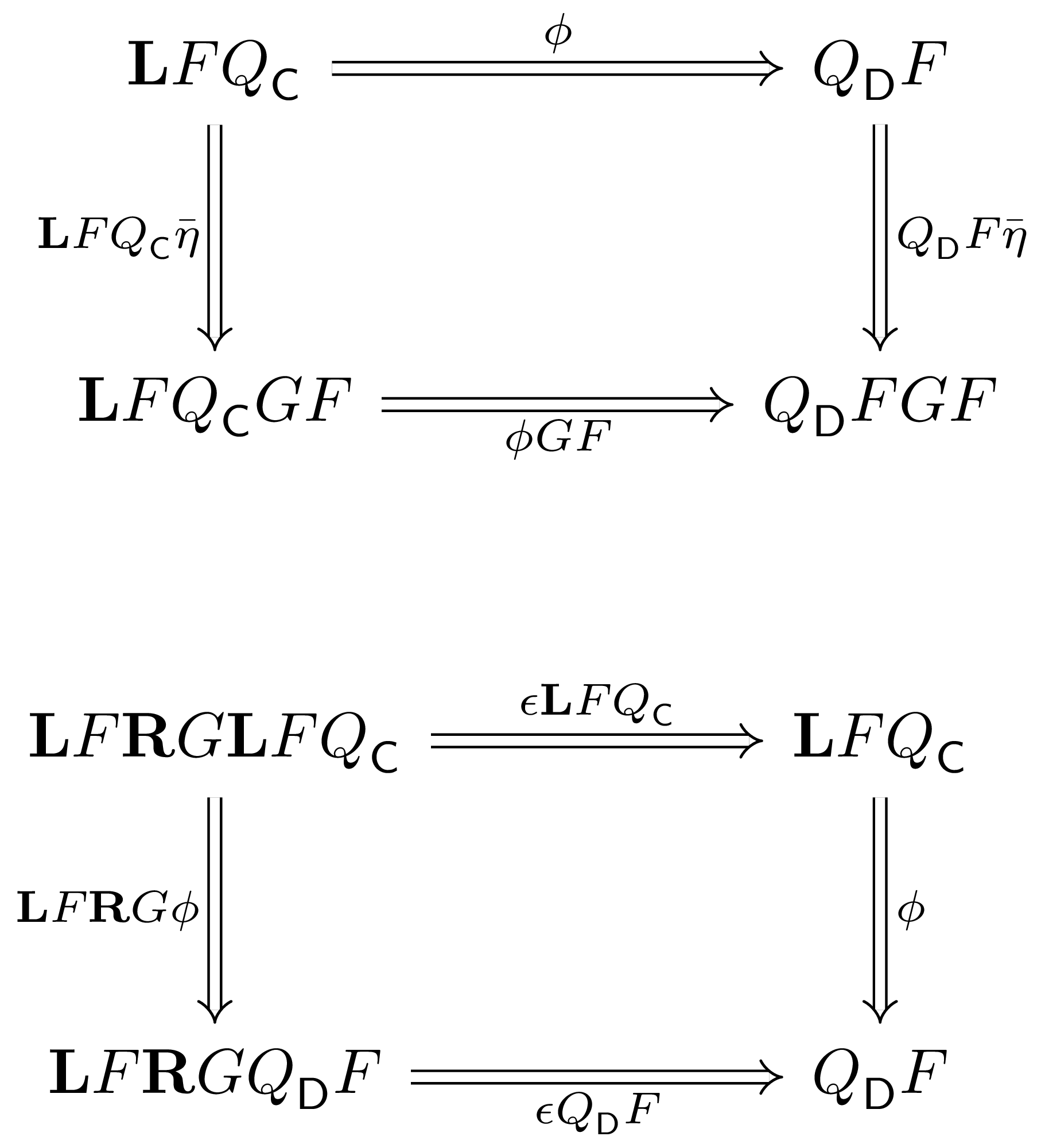
Uniqueness of this factorization demands $\eps\dL F\circ\dL F\eta = 1_{\dL F}$. Verification of the zig-zag identity $\dR G\eps\circ\eta\dR G= 1_{\dR G}$ proceeds similarly. $\square$
Extension Problems
-
Describe (co)limits in terms of Kan extensions. (There are at least two ways to do so; see Riehl 6.3.10 and 6.5.1).
-
Choose your favorite functor $K\co \C\to\Set$ that admits both a left and right adjoint. Express that functor as a precomposition functor between functor categoriesHint: think about mapping out of the terminal category $\1$., and compute the left and right adjoints of $K$ using the (co)limit formulas for Kan extensions and the fact that $\Lan_K\dashv K^*\dashv\Ran_K$.
-
Find an absolute Kan extension that is different from the Kan extensions induced by an adjunction.
-
State the universal property of Kan extensions precisely - that is, what is the category in which left Kan extensions are initial, and what is the category in which right Kan extensions are final?
-
Continuing from (4), over what diagrams are Kan extensions (co)limits?
-
Show that the 2-of-6 property implies the 2-of-3 property: If any two of $f$, $g$, or $gf$ are weak equivalences, so is the third. Use this to complete the proofs mentioned as "straightforward" in the homotopy section.
-
(For the programmers in the room.) Well-type what it means for a functor to a be a (left/right) Kan extension in your favorite functional language, making sure to encode the universal property. Then, choose your favorite functor, an extension, a Kan extension along that functor, and write a procedure to extract the universal property of the extension given any other functor.
Resources
I hope you enjoyed this quick introduction to Kan extensions. For further context, you may be interested in any of the resources below.